06. Largest Rectangle In Histogram
Given an array of integers heights representing the histogram's bar height where the width of each bar is 1,
return the area of the largest rectangle in the histogram.
[질문하기]
- 입력 배열이 비어있거나 height이 0일 수도 있나요?
- 히스토그램의 직사각형을 어떻게 정의하나요?
[아이디어]
- 더 작은 높이가 나오면 확장할 수 없으므로 직사각형의 넓이를 계산하고, 더 높은 높이가 나오면 확장할 수 있으므로 stack에 쌓자.
[풀이 1] Stack
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
stack = []
maxHeight = 0
for i in range(len(heights) + 1):
while stack and (i == len(heights) or heights[stack[-1]] > heights[i]):
oldIdx = stack.pop()
width = i if not stack else i - stack[-1] - 1
maxHeight = max(maxHeight, width * heights[oldIdx])
stack.append(i)
return maxHeight
히스토그램을 직접 그려서 영역을 옮겨가며 넓이를 구해보면, 어떤 고정된 영역을 기준으로 최소 height가 직사각형의 높이가 됨을 알 수 있다. 따라서 Brute Force의 아이디어는, "Idx를 하나씩 늘려가면서, 해당 Idx의 직사각형을 포함하는 가장 큰 직사각형의 넓이를 구하는 것"이다. 넓이를 계산할 때 특정 Idx에서의 직사각형을 포함하려면, height[Idx]보다 작은 높이가 나오면 안 된다. 따라서 왼쪽에서 Idx에서의 높이보다 작은 높이를 가진 LIdx, 오른쪽에서 Idx 높이보다 작은 높이를 가진 RIdx가 나올 때까지 확장해서 RIdx - LIdx - 1로 width를 구할 수 있다.
여기서 중복된 계산을 줄이는 Idea는 각 Idx마다 LIdx와 RIdx를 구하는 것이 아니라, Stack을 사용하여 각 SIdx에 대해 "이 SIdx에서의 높이가 직사각형의 최소 높이가 될 때까지" Idx를 확장해 주는 것이다.
즉, 지금 Idx에서의 높이가 Stack에 저장된 마지막 SIdx에서의 높이보다 크다면, Sidx에서의 높이는 여전히 직사각형의 최소 높이이므로 Idx를 저장해준다. 하지만 만약 Idx에서의 높이가 SIdx보다 작다면, SIdx가 최소 높이가 될 수 없으므로 pop 해주고, 그때의 직사각형의 넓이를 계산해 준다.
이때, SIdx를 pop해도 Stack에 원소가 있다면, 그것은 해당 Idx에서의 높이가 SIdx보다 작았었다는 것이기 때문에 그것이 곧 LIdx가 되고 만약 Stack이 모두 비었다면, 해당 SIdx에서의 높이가 전체 히스토그램에서의 최소 높이라는 의미이므로 width는 곧 Idx (배열의 최대 Idx)가 된다.
ex) [2, 1, 5, 6, 2, 3]
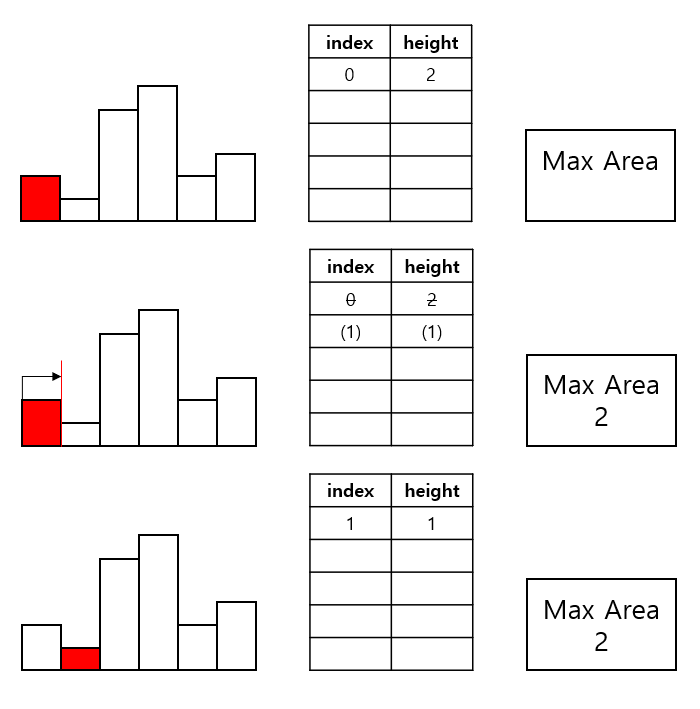
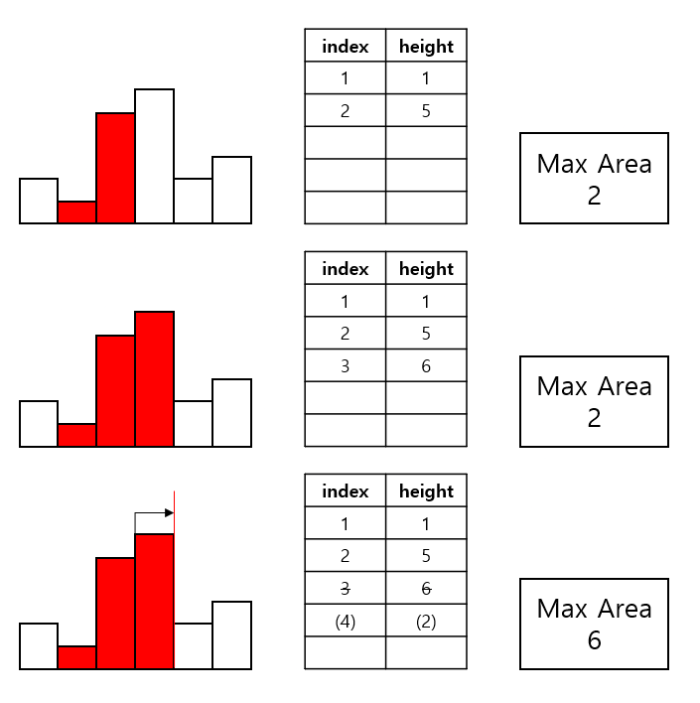
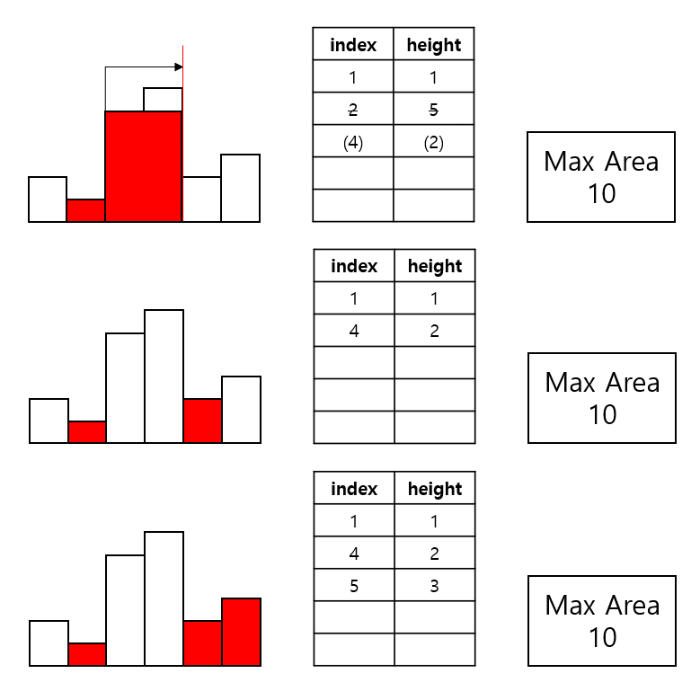
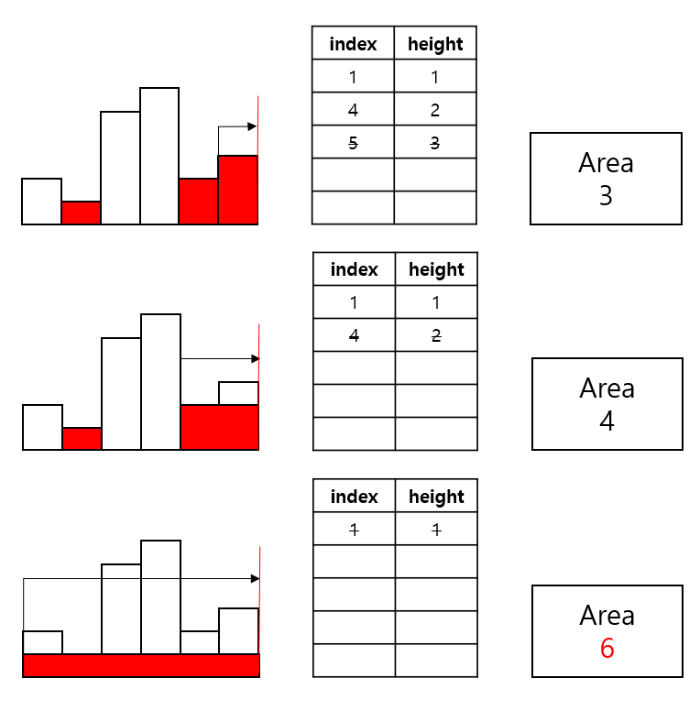
⏱️ 시간복잡도
배열을 한번 순회하기 때문에 시간 복잡도는 O(n)이다.
🧠 공간복잡도
최악의 경우 모든 Idx들이 stack에 쌓일 수 있으므로 공간 복잡도는 O(n)이다.
'자료구조와 알고리즘' 카테고리의 다른 글
| [DSA][Two Pointers] 02. Two Sum II - Input Array Is Sorted (1) | 2025.06.03 |
|---|---|
| [DSA][Two Pointers] 01. Valid Palindrome (1) | 2025.06.02 |
| [DSA][Stack] 05. Car Fleet (1) | 2025.05.31 |
| [DSA][Stack] 04. Daily Temperatures (0) | 2025.05.28 |
| [DSA][Stack] 03. Evaluate Reverse Polish Notation (0) | 2025.05.27 |
댓글