Floyd’s Cycle Detection Algorithm은 연결 리스트에서 사이클의 존재 여부를 확인하고, 사이클이 존재할 경우 사이클의 시작 지점까지 찾아낼 수 있는 알고리즘이다. 이 알고리즘은 두 개의 포인터를 사용하는데, 하나는 한 칸씩(slow), 다른 하나는 두 칸씩(fast) 이동하며 진행된다. 이러한 구조 때문에 Fast and Slow Pointer Algorithm, 또는 Tortoise and Hare Algorithm(거북이와 토끼 알고리즘)이라고도 불린다.
[알고리즘 구현]
# Definition for singly-linked list node.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
# 1. 사이클의 존재 여부 확인
def hasCycle(self, head: ListNode) -> bool:
tortoise = head # slow pointer
hare = head # fast pointer
while hare and hare.next:
tortoise = tortoise.next # 1칸 이동
hare = hare.next.next # 2칸 이동
if tortoise == hare: # 두 포인터가 만나면 사이클이 존재
return True
return False
# 2. 사이클의 시작 지점 찾기
def detectCycle(self, head: ListNode) -> ListNode:
tortoise = head
hare = head
while hare and hare.next:
tortoise = tortoise.next
hare = hare.next.next
if tortoise == hare: # 사이클이 있을 경우
tortoise = head # slow를 리스트의 시작으로 이동
while tortoise != hare: # 두 포인터가 만날 때까지
tortoise = tortoise.next
hare = hare.next
return tortoise # 사이클 시작 노드 반환
return None
- hasCycle 메서드
한 칸씩 이동하는 slow 포인터와 두 칸씩 이동하는 fast 포인터를 사용하여 순회한다.
순회 중에 두 포인터가 만나면 사이클이 존재한다고 판단한다. - detectCycle 메서드
hasCycle과 같은 방식으로 두 포인터가 만나는지 확인한다.
순회 중에 두 포인터가 만나면, slow 포인터를 연결 리스트의 시작 지점으로 옮긴 후 slow와 fast를 모두 한 칸씩 이동시킨다.
두 포인터가 다시 만나는 위치가 바로 사이클의 시작 지점이다.
[알고리즘 동작 원리]
[1] 왜 사이클이 존재하면 두 포인터가 만나는가?
직관적으로 생각하면, 만약 사이클이 없다면 fast 포인터가 먼저 연결 리스트의 끝(null)에 도달하므로 두 포인터가 만날 수 없다.
반대로 사이클이 존재한다면, fast는 결국 사이클 안에서 slow를 따라잡게 된다. 속도 차이(2배)로 인해 fast는 매 라운드마다 slow를 한 칸씩 더 빠르게 추격하며, 반드시 언젠가는 같은 노드에서 만나게 된다.
[2] 두 포인터가 만난 지점에서 하나의 포인터를 시작 지점으로 옮기고 각 포인터를 한 칸씩 이동했을 때 만나는 지점이 왜 사이클의 시작지점인가?
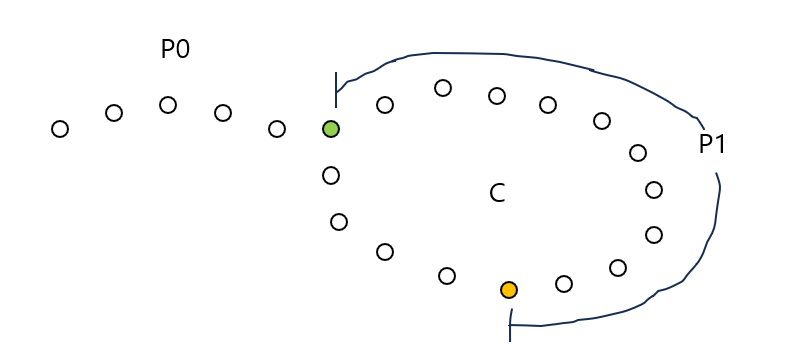
연결리스트의 시작 지점에서 사이클의 시작 지점까지 : P0
사이클의 시작 지점에서 두 포인터가 만난 지점까지의 거리 : P1
사이클의 길이 : C
가장 간단한 형태로 먼저 생각해 보자. 거북이가 한 칸씩 이동하는 동안 토끼가 사이클을 한 바퀴 돌아서 거북이를 따라잡았다고 생각해 본다면, 거북이가 P0 + P1을 이동하는 동인 토끼는 P0 + P1 + C만큼 이동했을 것이다. 토끼가 2배 빠르기 때문에 이동 거리도 2배일테니, 2(P0 + P1) = P0 + P1 + C이고 P0 = C - P1가 된다. 따라서 두 포인터가 만난 지점에서 P0 만큼 가면 사이클의 시작 위치가 된다.
조금 더 엄밀하게 살펴보자. slow가 이동한 총 거리가 P0 + P1이라고 하면, fast는 속도가 2배이므로 2(P0 + P1)만큼 이동했다.
이때 slow와 fast는 사이클을 한 번 이상 돌았을 수 있으므로, 이동 거리의 차이는 사이클 길이 C의 배수여야 한다.
P0 + P1 = kC (k는 양의 정수)
P0 = kC - P1이제 slow를 시작 지점으로 옮기고, fast는 그 자리(만났던 지점)에서 그대로 둔 채, 두 포인터를 같은 속도(1칸씩)로 이동시키면, slow는 P0만큼 이동하고, fast는 사이클을 따라 C - P1만큼 이동한다.
P0 = kC - P1
P0 = C - P1 (mod C)P0가 kC - P1이기 때문에 C - P1이다. 총 이동 거리가 아닌 위치의 개념으로 살피기 위해 mod 연산을 사용하면 사이클 내에서의 위치 상 kC = C이기 때문이다.
'자료구조와 알고리즘' 카테고리의 다른 글
| [DSA][Linked List] 05. Remove Nth Node From End of List (0) | 2025.06.30 |
|---|---|
| [DSA][Linked List] 04. Reorder List (0) | 2025.06.29 |
| [DSA][Linked List] 03. Linked List Cycle (1) | 2025.06.26 |
| [DSA][Linked List] 02. Merge Two Sorted Lists (0) | 2025.06.25 |
| [DSA][Linked List] 01. Reverse Linked List (0) | 2025.06.23 |

댓글